How should you use a magnifying glass?
Magnifying glasses operate on a pretty simple concept: when an object is within the focal length of a convex lens, a magnified ‘virtual’ image is produced, as demonstrated by simple ray optics:
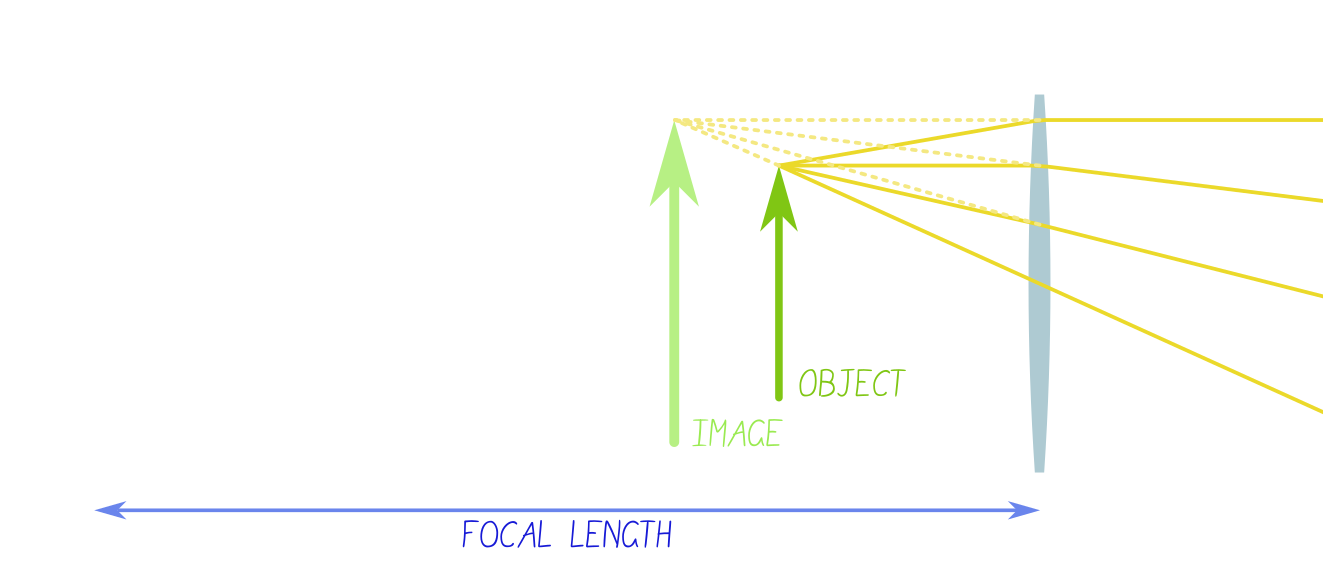
… with just the slight problem that the magnified image is always further away. An object at the focal point produces an image that is literally infinitely big – but it’s also at an infinite distance. And that really doesn’t help; the moon is quite sizeable itself, but that won’t show you the dust on its surface.
Still, magnifying glasses certainly seem to have an effect – but sometimes you just have to wonder, “How should I be using this, to get the biggest visible image I can?” Should the magnifying glass be near the object, near your face, somewhere in between? Where in between? Let’s find out.
In this regard the simple magnification of optics – the image divided by the object – won’t suffice. We need to consider that image size divided by its distance from your eye, to get an idea of the field of view it spans.[1] And although eyes can change their focus to a range of distances by a process called ‘accommodation’, you can’t focus on anything that’s too close, otherwise you could just press up directly against something and see it in immaculate detail. So we need to ensure the image-to-eye or accommodation distance is beyond some minimum. This ‘near point’ is not at all set in stone: it differs between individuals and gets considerably longer with age, such that could be between 60 to 600 mm even for ‘normal’, non-hyperopic vision. There’s also an aspect of comfort, as maintaining maximum accommodation for very close objects is legitimately strenuous.
Crunching the numbers for a range of lens-to-object and lens-to-eye distances gives the following:
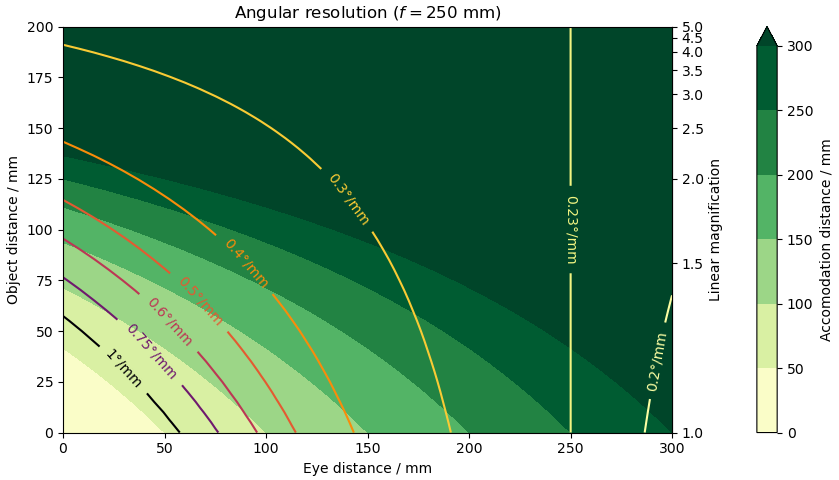
Image sizes and distances for a typical low-power magnifying glass, with focal length of 250 mm or 4 dioptres, often claiming ‘2× magnification’.
The shaded contours denote the resulting image distance, from zero in the bottom left towards infinity. Labelled contours show the resulting visual size, such that a bigger value always shows more detail. The bottom edge, where object separation from the lens is zero, also corresponds to zero image separation and unity magnification, i.e. the situation where the magnifying glass is completely absent.
It can be seen that closer images generally occupy a larger field of view, which is not really surprising. However, by looking along any given accommodation contour, you can see that the apparent size of the image consistently increases as the object gets further from the glass and the eye gets closer. So the optimal approach is: press the glass right against your eye, as close as you can, then get the object (and thus the image) at the minimum distance where you can still focus on it. If you want to relax your eye a little bit by having the image a bit further away, it’s still optimal to have the glass up against your face and just have the object a bit further away, where you can look at it comfortably. Problem solved!
A point of interest: when maintaining a smaller accommodation distance, the difference between optimal magnification and no magnification is much smaller than for more distant images. For example, the 300 mm accommodation passes through 0.2°/mm and beyond 0.4°/mm, giving more than double the improvement, while at 100 mm the improvement is only 1.4 times. This trend is shown in detail in the following plot:
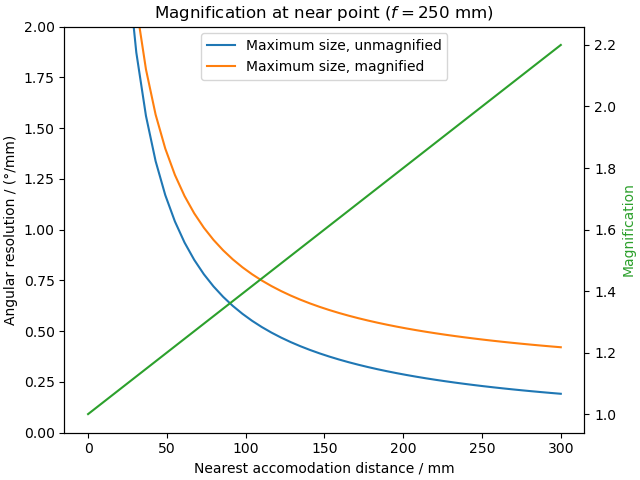
Which is a phenomenon I had no idea about. Generally I’ve never found magnifying glasses to be particularly impressive, and certainly not to offer anything like 2× magnification. But it turns out that, if you can already focus on objects fairly close to your eye, the relative difference a magnifying glass makes is not so great. Often in optics an accommodation distance of 250 mm is assumed, and in this situation a 250 mm magnifying glass does indeed show objects twice as big. But if you can focus on something closer, such as at 125 mm, the same magnifying glass only provides 1.5× magnification when used at that distance.
In fact, what the magnifying glass does for any given accommodation is to provide a constant additive increase to the angular resolution, equal to . For a 250 mm focal length, that’s 0.004 rad/mm, or an extra 0.23° for every millimetre of object size. That’s only when being careful to maintain the same necessary accommodation with and without magnification, though.