Paths of constant bearing (known as ‘loxodromes’ or ‘rhumb lines’) are often mentioned in the context of the Mercator projection, as they are always straight lines on the map. It’s often emphasised that this is not the shortest route between two locations, but something I feel is glossed over is the direct consequence that these paths are not straight on a sphere, even though the bearing is consistent. In general, following a steady course on a compass requires turning slightly along the entire journey. Perhaps the most obvious indication of this is to imagine travelling due east when only a metre from a pole – evidently you would have to veer significantly to the side to keep from travelling all the way to the other side of the planet.

The topological measure of this turning is ‘geodesic curvature’, which generalises straight and not-straight curves to non-flat surfaces and beyond Geodesics, which are the shortest paths between two points, have zero geodesic curvature, but the notion of geodesic curvature provides a straightforward way to sensibly extend geodesics beyond the point where a different path would be the shortest route between its endpoints. On a sphere, geodesics are great circles such as the equator and lines of longitude, which means they are the equivalent of straight paths and following them requires no turning. It could also be considered that following the equator eastwards is exactly halfway between turning left around the north pole and turning right around the south pole – zero turning.

So if following a compass necessitates turning to the side, the natural question is, how much turning? Unfortunately, the interwebs are strangely silent on this matter – with the exception of Wolfram MathWorld, which helpfully offers “The arc length, curvature, and torsion are all slightly complicated expressions.” Thanks! We’ll just have to do this the hard way.

There are various ways of calculating geodesic curvature, but ultimately it all hinges on the second derivative of the curve. Which isn’t pretty, but it is doable.

First, a loxodrome parameterised by distance along the loxodrome from the equator is given by:

Hence:

Where $s$ is the distance from the equator, $\beta$ is the bearing from north, $\varphi$ is latitude, $\lambda$ is longitude, and ${\mathrm{gd}}^{-1}\varphi ={\int }_0^{\varphi }\sec t\mathrm{d}t$ is the inverse Gudermannian function.

A point along the curve and its first two derivatives are thus:

If that was fun to read, it was even more fun to derive, write and transcribe. Really.

After all that, a straightforward way to yield geodesic curvature is to find the dot product of $𝐫\prime \prime$ with the following vector:

Which is just $𝐫\prime$ with $\beta$ rotated by $\frac{\pi }{2}$.

The ultimate result is something as follows:

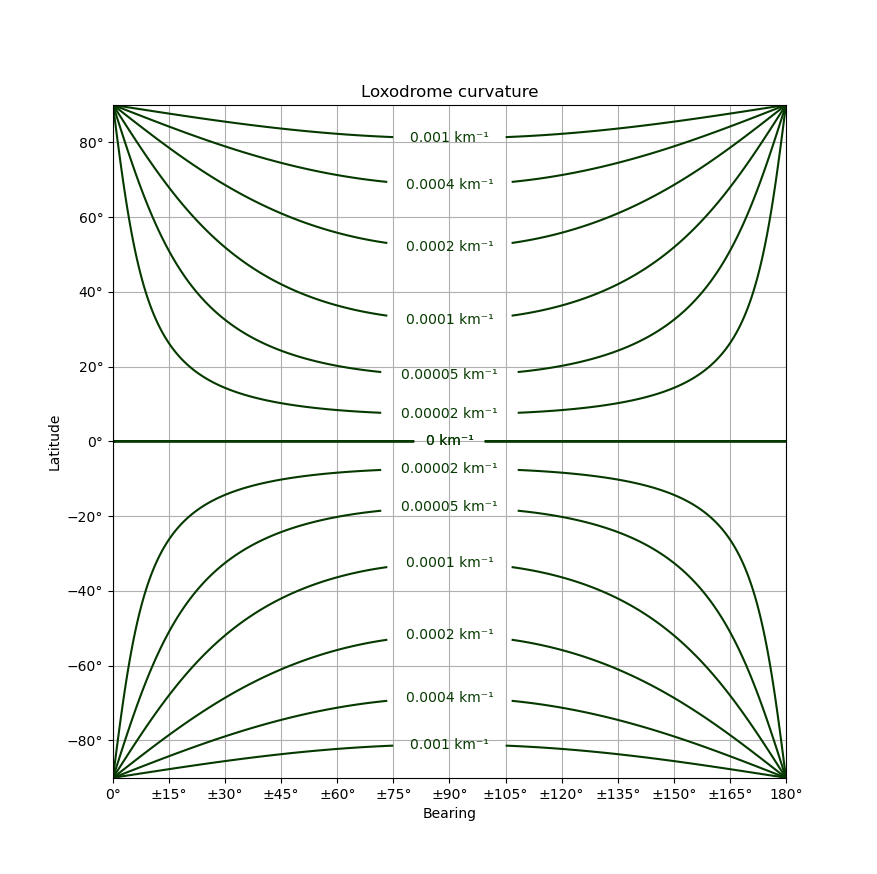
Following a loxodrome involves moving vertically along this chart at a consistent rate. The curvature is always away from the equator and toward the closest pole – so travelling eastwards in the northern hemisphere or westwards in the southern hemisphere both involve turning left. The values for curvature can be understood as the reciprocal radius of a circle being followed at that point, but note it’s a planar circle and not one whose radius is measured along the surface of the earth. Zero curvature in this context would be tracing an infinite circle that degenerates to a straight line.

So as an example, heading northeast at latitude 60° south requires slowly turning to the right (southeast) to follow a circle 1/(0.0002 km⁻¹) = 5000 km in radius. Making this turn is necessary to stay on a northeast heading, otherwise the figure of the earth would have the path measured increasingly northward as it approaches the equator.