The ‘artificial gravity’ of a rotating spacecraft is a recurring trope across science fiction. Centrifugal force is a real and necessary effect in a rotating reference frame, but the description of motion is incomplete without Coriolis force alongside it. Unfortunately, the latter doesn’t get much representation in fiction that I’m aware of.

Coriolis force pushes sideways on objects that move in the plane of rotation of the rotating reference frame, causing them to move in arcs. Coriolis effects are perhaps best known in the context of atmospheric wind: as the Earth and its atmosphere form a rotating reference frame, the large-scale motion of air experiences force sideward force (relatve to the Earth) that counters pressure gradients in the air, and allows vortices to remain fairly stable over long periods of time rather than quickly collapsing.

In a rotating reference frame with angular velocty $\omega$, an object moving in the plane of rotation with velocity $v$ experiences a Coriolis acceleration of $2\omega v$ orthogonal to its velocity and the axis of rotation.[1] When you toss a ball straight up in the air, on an Earth spinning at $0.000073{\mathrm{s}}^{-1}$, it swings to the west very very slightly… but with so many leading zeros in the angular velocity, it’s not something you’d ever notice. Driving across the south pole at 100 km/h, you would be pushed to the right with a force 5000 times weaker than gravity.

This is not so the case on centrifugal spacecraft. They have to spin faster to have a centrifugal effect worth bothering, and that means Coriolis forces get bigger too.

Here’s the same animation viewed from an inertial reference frame:

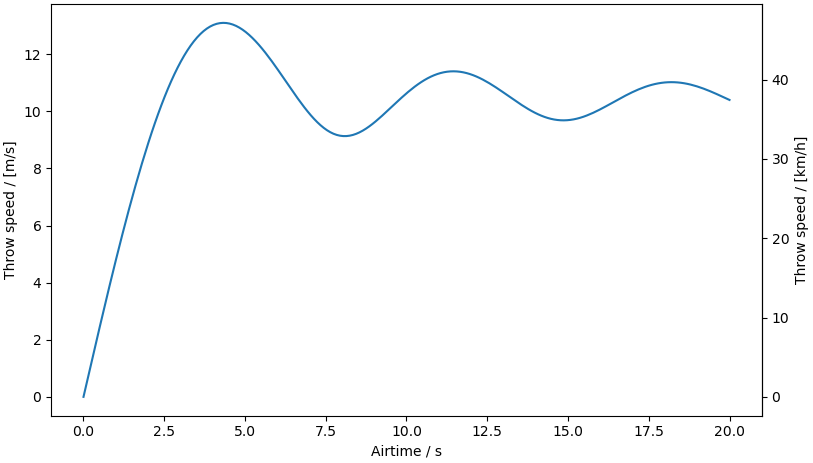
So throwing something to yourself is a bit more involved than tossing it straight up. But a neat efect is you can actually achieve arbitrary airtime with a limited launch velocity – in this case, no more than 13 m/s, and approaching 10.4 m/s for indefinite airtime.

Other fun Coriolis Considerations: ascending the ladder to reach the middle would cause you to be pushed to the right as long as you were climbing. Supposing a 1 m/s ascent, that would be a push of about 0.95 m/s², or a tenth the force of Earth gravity. That would make the ground feel slightly tilted at the bottom, then as you ascended, the centrifugal component would steadily decrease so you’d be ‘climbing’ more and more sideways. Similarly, descending the ladder would result in being pushed to the left. If you got to the top and let go, you would slowly fall down… and then swing around to the left, doing bigger and faster loops around the interior until skidding along the ‘ground’ at about 10 m/s, which could be quite unpleasant. The railings are for your safety.

Another fun phenomenon owing to centrifugal force is its dependence on radial distance. The effective gravity at the edge might be that of Earth’s surface, but a mere two metres up it’s down to about eighty percent of that – your feet would be a fair bit heavier than your head. All of these ‘anomolies’ are diminished as the angular velocity is reduced, resulting in either weaker ‘gravity’ throughout or the need for a larger radius.