It’s a simple fact of life that everyone loves the azimuthal equidistant projection, which shows the world at the correct distance and direction from its central point, even those who have never seen the term in their life.

For example, when centred on Sydney:

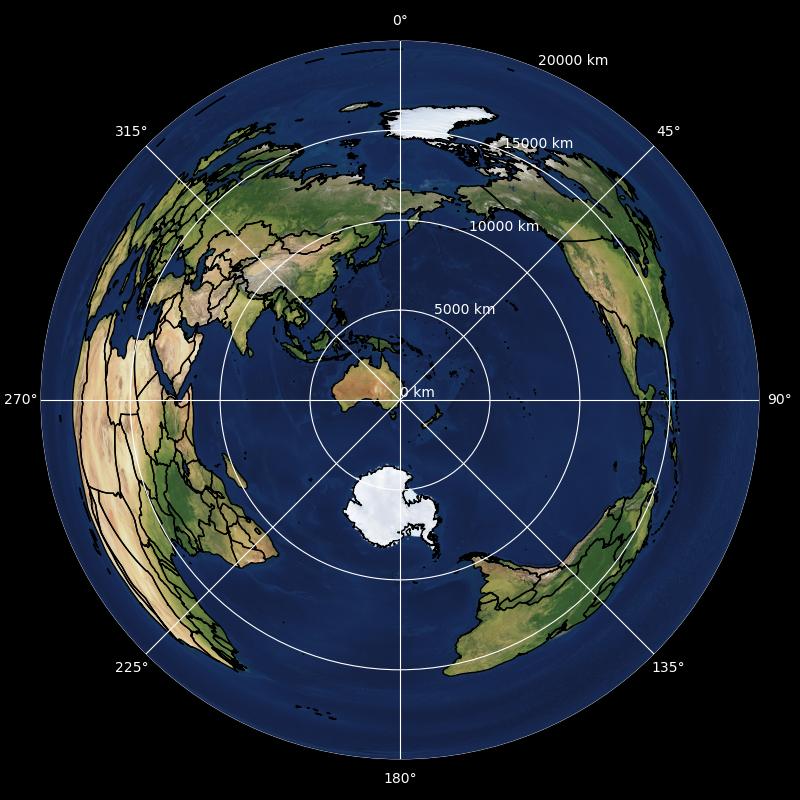
One particular point of interest is that Cuba is shown east of Sydney, despite being in opposite hemispheres. And while this is literally true…

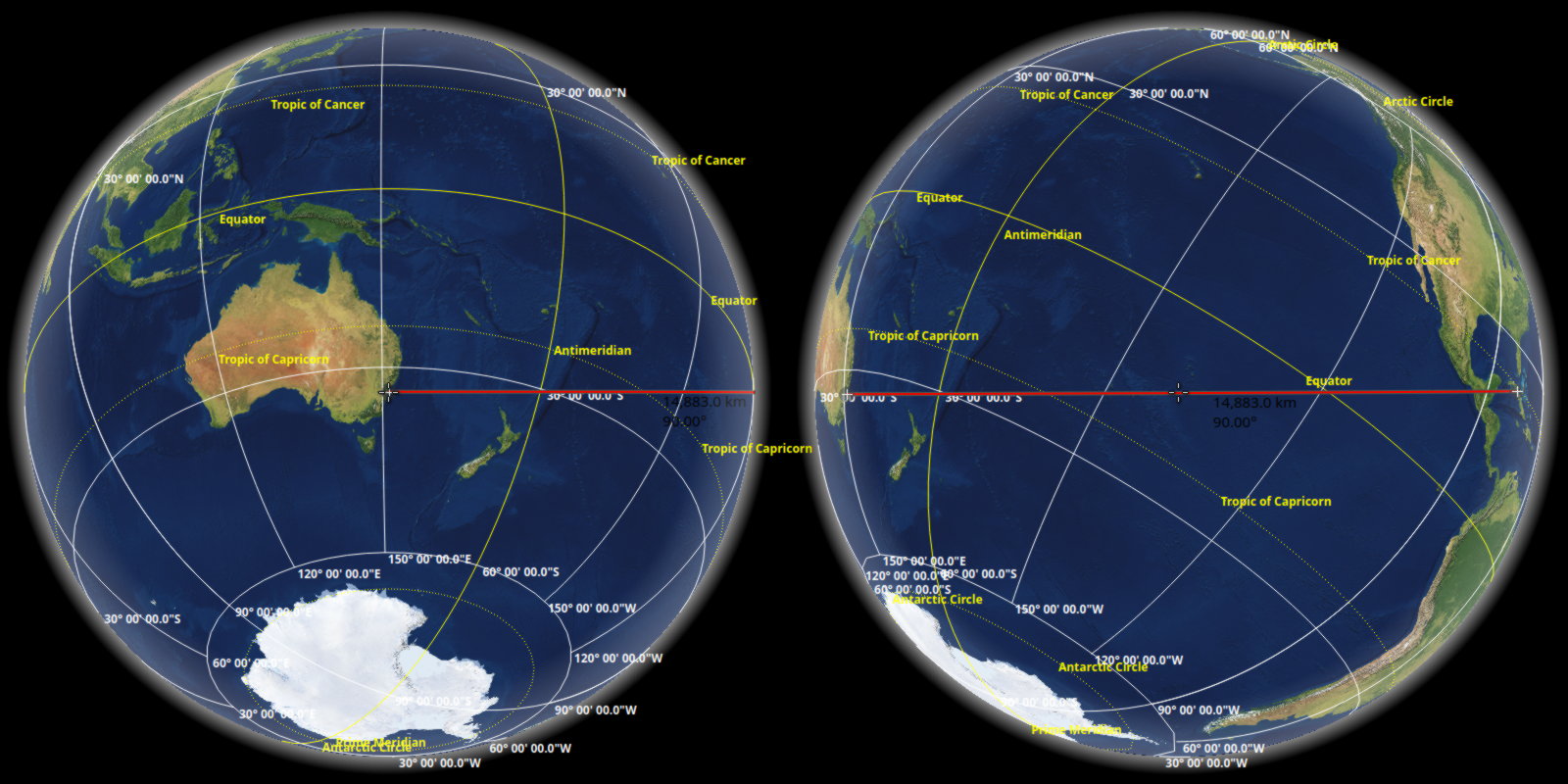
It doesn’t do much to affirm ill-conceived views of the world perpetuated by cylindrical and pseudocylindrical maps. Wouldn’t it be nice to use terrible metrics for ‘distance’ and ‘direction’ that show all objects on the central latitude along a horizontal line, such that nobody might inadvertently develop a better understanding of spherical geometry? Obviously, it would.

In the cardinal directions, this is simple. North and south should be measured along the central meridian, while east and west should be measured along the central parallel. The challenge comes in generalising some curve to all bearings, with meridians and parallels as limiting cases.

My first thought was to use loxodromes (rhumb lines) – curves that follow a constant bearing. Conceptually this is simple enough, and it turns out that measuring the bearing of and distance along a loxodrome between two points is fairly straightforward. Loxodromes are also all uniformly straight lines under the much-maligned Mercator projection, implying the lovely name of ‘Mercatorial equidistant’ – a map that effectively scales the Mercator projection along lines through the central point to maintain their scale. So one Sunday afternoon I hacked just this together.

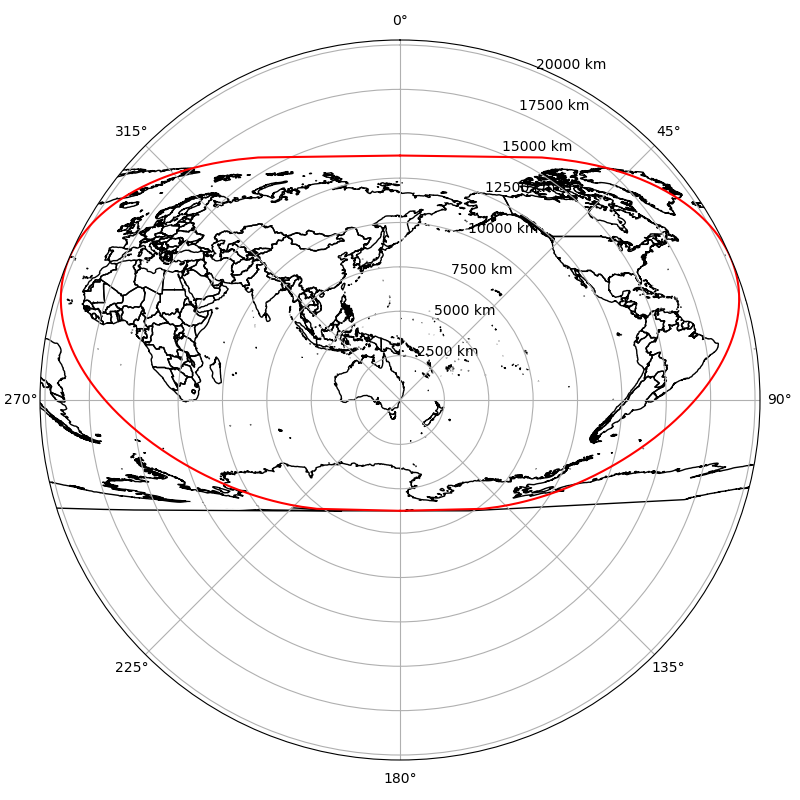
Mission accomplished, right? Unfortunately it looks disturbingly pseudocylindrical – in fact it is pseudocylindrical. I’m not entirely sure why, but despite being measured from a single point, all parallels end up being straight (and… parallel) with consistent (but differing) scales, which just so happens to be the defining characteristic of a pseudocylindrical projection. And you can’t really exacerbate (pseudo)cylindrical confusion with a map that is literally (pseudo)cylindrical.

Even more disappointingly, this projection just so happens to

1. Already exist under the name ‘loximuthal’

2. Be present in my browser history

which I was only tipped off to after seeing those devastatingly straight parallels and investigating further (and thus learning that they are indeed actually straight, instead of merely looking the part). It was at this point that I didn’t bother to add a pretty basemap. Incidentally, the bastion of all knowledge that is Wikipedia notes that the loximuthal projection was “introduced by Karl Siemon in 1935, and independently in 1966 by Waldo R. Tobler,” and I eagerly await being added to this list.

But the original goal is still open. To be less disappointing, it just needs a different class of curve that meridians and parallels are a subset of. One solution to this is spherical circles. Spherical circles are probably quite self-explanatory – you draw a circle on a sphere. Meridians, as parts of great circles through the poles, and parallels, as small circles around the poles, are both spherical circles. And these two circles both intersect at the central point and a single other point, with the same latitude and opposite longitude. Thus, take two: measuring distance and direction along spherical circles through the central point and its longitudinal antipode. This is enough! Those two points and any other point on the globe define a unique spherical circle that can measure distance and direction, and results in the central meridian or parallel when the third point is also on that meridian or parallel.

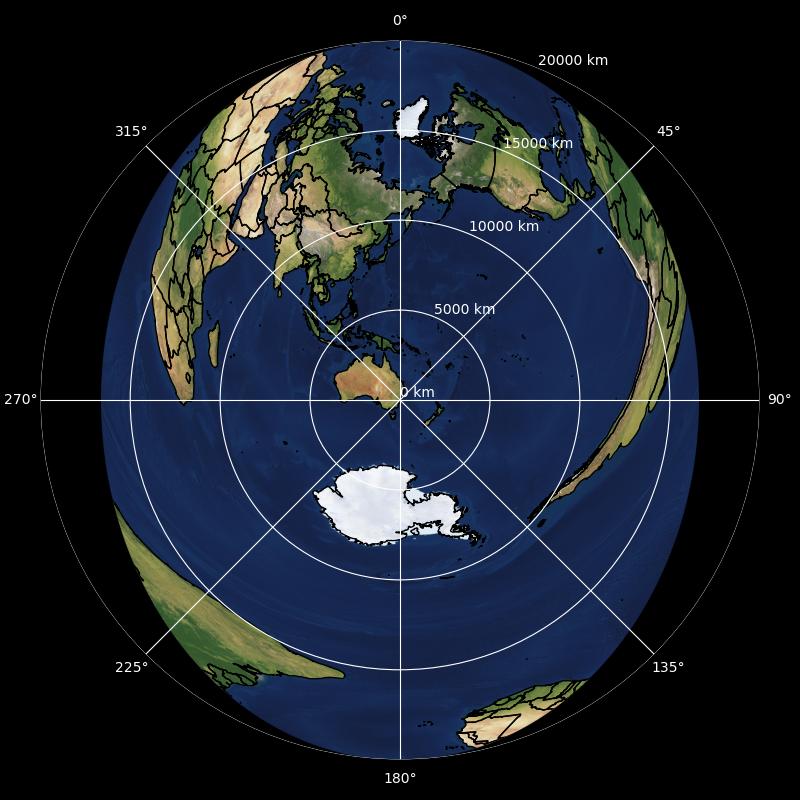
The result is delightfully obtuse. The centre of the map looks fairly normal, Cape Town and Buenos Aires are vertically aligned with the middle just as they shouldn’t be, and the rest of the map is horrifically warped to accomodate them. The effect is amplified as the central point moves away from the equator, making the map increasingly narrow. Perhaps the biggest downside is that the boundary of the map cuts continents in fairly arbitrary ways, although it is possible to shift the boundary in a way that it represents a single point as in normal whole-world azimuthal projections, with the effect of moving the central point away from the centre.

Note that the approach could be generalised to some other class of spherical circle by using a different common point. The normal azimuthal equidistant projection is the limiting case when all circles pass through the actual antipode of the central point, thus becoming great circles. With a different framing, this leads to flat-Earth style maps where an arbitrary point encompasses the entire border, and a completely unrelated arbitrary point has no distortion (but is generally not centred).

And as far as I’m aware, this is, so far, not preceded by prior art.